The Ziegler–Nichols tuning method is a heuristic method of tuning a PID controller. It was developed by John G. Ziegler and Nathaniel B. Nichols. It is performed by setting the I (integral) and D (derivative) gains to zero. The 'P' (proportional) gain, is then increased (from zero) until it reaches the ultimate gain, which is the largest gain at which the output of the control loop has stable and consistent oscillations; higher gains than the ultimate gain have diverging oscillation. and the oscillation period are then used to set the P, I, and D gains depending on the type of controller used and behaviour desired:
| Control Type | |||||
|---|---|---|---|---|---|
| P | – | – | – | – | |
| PI | – | – | |||
| PD | – | – | |||
| classic PID[2] | |||||
| Pessen Integral Rule[2] | |||||
| some overshoot[2] | |||||
| no overshoot[2] |
The ultimate gain is defined as 1/M, where M = the amplitude ratio, and .
Apr 26, 2018 “ One of my key components to a successful mix on every song is the Waves C1 sidechain plugin. This simple plugin is one of the fastest ways to both capture clarity and gain control of the vocals. I like to have the plugin set up in Split mode with the EQ type set to Band Reject. Waves C1 Comp-gate Download - DOWNLOAD (Mirror #1). Vst plugin waves c1 compressor download. Download VST Plugins Free VST, Plugins, Audio, Samples, Free, Download. Download VST Free Waves 11 Full Bundle (Win) Waves Mercury V11 Free Download (Mercury, SSL, Abbey Road, MultiRack) Download link at the end of the page. 165 plugins and more than 400 components, From Waves in one package. C1 Compressor Free Download; C360 Surround. C1 Compressor by Waves (@KVRAudio Product Listing): The C1 is a frequency-selective dynamic processor allowing two simultaneous dynamic processes. It is an expert tool for any application requiring compression, expansion or gating. Select any frequency range, then apply a dynamic process to that range, or use as a traditional wideband device. Get C1 Compressor by Waves and learn how to use the plugin with Ableton Live, Logic, GarageBand, and FL Studio for free. Discover 20+ world-class professional VST/AU music plugins like Serum, Arturia’s V Collection, iZotope’s Ozone, & Presonus’ Studio One DAW.
Point for improving the performance of PID controllers. It offers an introduction to both the art and the science behind process control and PID controller tuning. Included are basic terminology, steps for analyzing process dynamics, methods for determining model parameters, and other valuable insights. With these fundamentals we.
These 3 parameters are used to establish the correction from the error via the equation:
Pid Auto Tuning Methods For Sale
How boot camp for mac works. which has the following transfer function relationship between error and controller output:
Evaluation[edit]
The Ziegler–Nichols tuning (represented by the 'Classic PID' equations in the table above) creates a 'quarter wave decay'. This is an acceptable result for some purposes, but not optimal for all applications.
This tuning rule is meant to give PID loops best disturbance rejection.[2]
It yields an aggressive gain and overshoot[2] – some applications wish to instead minimize or eliminate overshoot, and for these this method is inappropriate. In this case, the equations from the row labelled 'no overshoot' can be used to compute appropriate controller gains.

References[edit]
- ^Ziegler, J.G & Nichols, N. B. (1942). 'Optimum settings for automatic controllers'(PDF). Transactions of the ASME. 64: 759–768.Cite journal requires
journal=(help) - ^ abcdefZiegler–Nichols Tuning Rules for PID, Microstar Laboratories
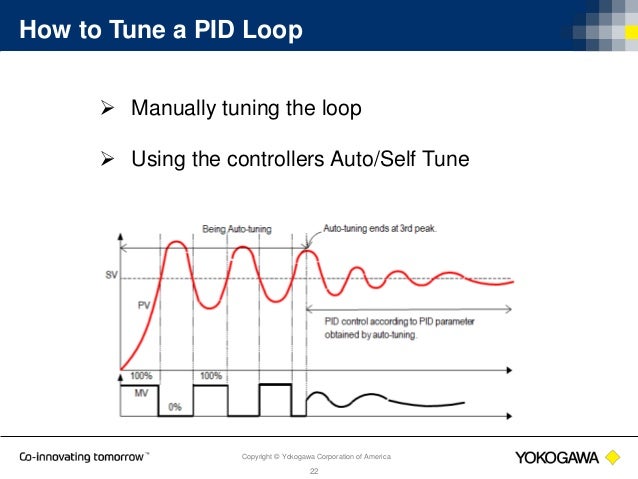
- Bequette, B. Wayne. Process Control: Modeling, Design, and Simulation. Prentice Hall PTR, 2010. [1]
- Co, Tomas; Michigan Technological University (February 13, 2004). 'Ziegler–Nichols Closed Loop Tuning'. Retrieved 2007-06-24.